CLASS 6 CHAPTER 4: BASIC GEOMETRIC IDEAS

EXERCISE 4.1

1.      Use the figure to name:

(a) Five points

(b) A line

(c) Four rays

(d) Five line segments

Solution

            

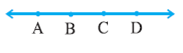
2.      Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.

 

Solution

 

3.      Use the figure to name:

(a) Line containing point E.

(b) Line passing through A.

(c) Line on which O lies

(d) Two pairs of intersecting lines.

Solution

4.      How many lines can pass through

(a) one given point?

(b) two given points?

Solution

a)      Infinite number of lines can pass through a single point.

b)      Only one line can pass through a single point.

5.      Draw a rough figure and label suitably in each of the following cases:

   

Solution

a)        

 

    b)       

    
       

    c)       

    
            

     d)       

 

6.      Consider the following figure of line MN. Say whether following statements are true or false in context of the given figure.

  

 

 Exercise 4.2

1.      Classify the following curves as (i) Open or (ii) Closed.

 

Solution

(a)    Is an open curve

(b)   Is an open curve

(c)    Is an open curve

(d)   Is a closed curve

(e)    Is a closed curve

2.      Draw rough diagrams to illustrate the following: (a) Open curve (b) Closed curve.

(a)    Open curve

(b)   Closed curve

3.      Draw any polygon and shade its interior.

4.      Consider the given figure and answer the questions:

(a)    Is it a curve? (b) Is it closed?

Solution

(a)    Yes, it is a curve.

(b)   Yes, it is a closed curve.

5.      Illustrate, if possible, each one of the following with a rough diagram:

(a) A closed curve that is not a polygon.

(b) An open curve made up entirely of line segments.

(c) A polygon with two sides.

Solution

(a)

     

 

(b)    

 

(c)    Not possible

Exercise 4.3

1.      Name the angles in the given figure.

 Solution

<ABC, <BCD, <CDA, <DAB

2.      In the given diagram, name the point(s)

 

(a) In the interior of <DOE

(b) In the exterior of <EOF

(c) On <EOF

           

Solution

a)      A

b)      C, A and D

c)      B, E, O and F

3.      Draw rough diagrams of two angles such that they have

(a)    One point in common.

 

<POR and <QOR have R in common.

(b)   Two points in common.

 

<POR and <QOR have points M and R in common.

(c)    Three points in common.

 

<POR and <QOR have points N, M and R in common.

(d)   Four points in common.

<POQ and <ROQ have points S, N, M and Q in common.

(e)    One ray in common.

 

Ray OR is common.

  

Exercise 4.4

1.      Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?

Solution

The point A lies on the triangle.

2.       

(a) Identify three triangles in the figure.

(b) Write the names of seven angles.

(c) Write the names of six line segments.

(d) Which two triangles have ∠B as common?

Solution

a)      ΔABD, ΔADC and ΔABC

b)      <ABD, <BDA, <ADC, <DCA, <CAB, <CAD, <DAB

c)      

d)     ΔABD and ΔABC

Exercise 4.5

1.      Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?

Solution

 

The diagonals PR and QS meet at O.

The point O is in the interior of the quadrilateral.

2.      Draw a rough sketch of a quadrilateral KLMN. State,

(a) two pairs of opposite sides,

(b) two pairs of opposite angles,

(c) two pairs of adjacent sides,

(d) two pairs of adjacent angles.

Solution

 

Exercise 4.6

1.      From the figure, identify:

 

(a)    the centre of circle

O is the centre of the circle.

(b)   three radii

OA, OB and OC

(c)    a diameter

AC

(d)   a chord

ED

(e)    two points in the interior

O and P

(f)    a point in the exterior

Q

(g)   a sector

OAB (shaded portion)

(h)   a segment

Segment ED (shaded portion)

2.      (a) Is every diameter of a circle also a chord?

     Yes

(b)   Is every chord of a circle also a diameter?

      No

     3. Draw any circle and mark

        (a) its centre

        (b) a radius

        (c) a diameter

        (d) a sector

        (e) a segment

        (f) a point in its interior

        (g) a point in its exterior

        (h) an arc

         Solution

a)      C is the centre of the circle

b)      is the radius.

c)      is a diameter

d)     CAP is a sector

e)      PB is a segment

f)       D is a point in the interior of the circle

g)      E is a point in the exterior

h)      

4. Say true or false :

(a) Two diameters of a circle will necessarily intersect.

      True

(b) The centre of a circle is always in its interior.

      True